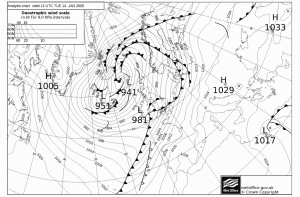
5th May: Storm Brendan Revisited
In my “Tidal Surge Forecasts” post (originally prepared for the NCI Calshot “Blog”) I used the tide heights observed during storm Brendan to illustrate that by increasing the water depth, storm surges resulted in the tide arriving earlier than in the Tide Tables.
In a further Calshot “Blog” post I explained how one could use the NTSLF storm surge residual forecast for Portsmouth to make an estimate of the total tide height to be expected in Southampton. I emphasised that it was important to use the forecast storm surge residual for the time of high tide and ignore the larger residual peaks which are caused by the early arrival of the tide.
Of course one could also estimate the surge at the time of low tide provided that the period during which the tidal height is relatively constant is greater than the number of minutes by which the tide is advanced. Knowing the surge height at low tide is less useful for flood prediction but might be useful, for example, when playing cricket on the Bramble Bank!
In “Tidal Surge Forecasts” I assumed that the surge was a constant 0.6m and arrived 15 minutes early. However Storm Brendan had peaked over Southampton on the 14th January and by the time of high tide in the early hours of 15th January the associated storm surge was decreasing in amplitude. Thus simulating the surge with a constant value did not result in a good fit.
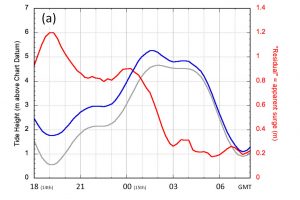
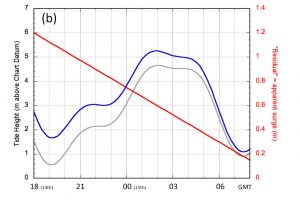
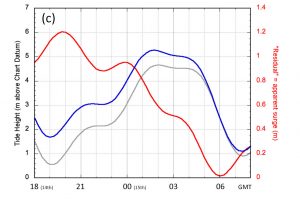
Looking again at the time period from 18gmt on the 14th January to 08gmt on the 15th, graph (a) shows the observed water depth at the Docks tide gauge (from Sotonmet) and the corresponding surge residual (the observed height minus the astronomical tide). Based on the surge values at low and high tide I defined a linear storm surge residual going from 1.2m at 18gmt/14th to 0.6m at 02gmt/15th. The corresponding water depths (graph (b)) look similar to those observed although, of course, the linearly decreasing residual looks unrealistic! Advancing the tide by 15 minutes resulted in variations in the storm surge residual that were significantly greater than those observed. However, assuming the tide arrived 10 minutes early gave the results shown in graph (c).
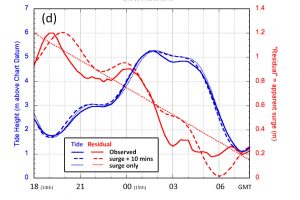
Comparison of the water depths and surge residuals calculated with and without advancing the tide by 10 minutes.
For this, storm Brendan, example, whilst advancing the time of arrival of the tide reproduces (and explains) the peaks in the storm surge residual, it is not obvious that the accuracy of the calculated water heights are much changed. This is illustrated in graph (d). Assuming a 10 minute advance did produce better agreement around the period of high water but not when the tide was lower.
In fact one can use the peaks in the residual over and above the actual surge value to estimate the amount the the tide is arriving early since:
 Using the values for the midnight peak when the storm surge residual was 0.84 (that is about 0.16 in excess of my linearly decreasing surge estimate) coupled with the observed rate of depth increase gives about 8.5 minutes tidal advance. Changes from the predictions shown in graph (d), which assume 10 minutes, were not significant.
Using the values for the midnight peak when the storm surge residual was 0.84 (that is about 0.16 in excess of my linearly decreasing surge estimate) coupled with the observed rate of depth increase gives about 8.5 minutes tidal advance. Changes from the predictions shown in graph (d), which assume 10 minutes, were not significant.
Conclusion, the storm surge initiated by storm Brendan had decrease by half or more by the early morning tide on the 15th January, being about 0.6m at the time of high water, and the tide arrived about 10 minutes early at the docks tide gauge compared to the astronomical tide.